Understanding Number Systems and Conversions
Understanding Number Systems and Conversions
Introduction Number System Conversion
Binary To Decimal & Vice versa
Binary to Octal & Vice Versa
Binary to Hexadecimal & Vice Versa
Decimal to Octal & Vice Versa
Decimal To Hexadecimal & Vice versa
Octal to Hexadecimal & Vice versa
Binary To Decimal Conversion
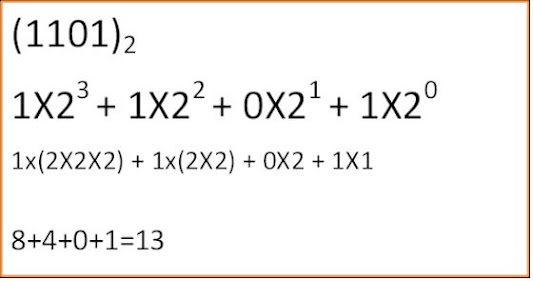 |
| Binary To Decimal Conversion |
Decimal To Binary Conversion
 |
| Decimal To Binary Conversion |
Octal to Decimal numbers Conversion
 |
| Octal to Decimal numbers Conversion |
Decimal to Octal Conversion:
 |
| Decimal to Octal Conversion: |
Hexadecimals to Decimal numbers Conversion
To convert a hexadecimal number to a decimal number, you follow these steps:
Step 1: Write down the hexadecimal number.
Step 2: Assign a position value to each digit of the hexadecimal number, starting from the right and increasing by a power of 16 for each position to the left. The rightmost digit is in the 16^0 position (which equals 1), the next digit to the left is in the 16^1 position (which equals 16), then 16^2 (which equals 256), and so on.
Step 3: Convert any letters in the hexadecimal number to their corresponding decimal values (A is 10, B is 11, C is 12, D is 13, E is 14, and F is 15).
Step 4: Multiply each digit of the hexadecimal number (including the converted letters) by its corresponding position value.
Step 5: Sum up all the products obtained in Step 4.
Step 6: The result is the decimal equivalent of the given hexadecimal number.
Let's take an example to illustrate the process. We'll convert the hexadecimal number 1A3 to its decimal equivalent:
Step 1: The hexadecimal number is 1A3.
Step 2: Assign position values: 3 is in the 16^0 position, A is in the 16^1 position, and 1 is in the 16^2 position.
Step 3: Convert the letter A to its decimal value, which is 10.
Step 4: Multiply each digit by its position value:
3 * 16^0 = 3 * 1 = 3
A * 16^1 = 10 * 16 = 160
1 * 16^2 = 1 * 256 = 256
Step 5: Add up the results: 3 + 160 + 256 = 419
Step 6: The decimal equivalent of the hexadecimal number 1A3 is 419.
So, the hexadecimal number 1A3 is equal to the decimal number 419.
Decimal to Hexadecimal Conversion
 |
| Decimal to Hexadecimal Conversion |
Frequently Asked Question(FAQ)
How to convert Binary no to decimal no ?
To convert a binary number to a decimal number, follow these steps:
Step 1: Write down the binary number.
Step 2: Identify the place value of each digit in the binary number. The rightmost digit represents the "ones" place, the next digit to the left represents the "twos" place, then the "fours" place, "eights" place, and so on, increasing by a power of 2 as you move from right to left.
Step 3: Multiply each digit by its corresponding place value.
Step 4: Add up all the results from Step 3 to get the decimal equivalent.
How to convert Decimal no to Binary no?
Step 1 Divide the decimal number by 2.
Step 2 Record the remainder (it will be either 0 or 1).
Step 3Repeat the division with the quotient obtained in the previous step until the quotient is 0.
Step 4 The binary representation is the sequence of remainders read in reverse order.
How to convert Octal no to decimal no ?
Step 1: Write down the octal number.
Step 2: Assign a position value to each digit of the octal number, starting from the right and increasing by a power of 8 for each position to the left. The rightmost digit is in the 8^0 position (which equals 1), the next digit to the left is in the 8^1 position (which equals 8), then 8^2 (which equals 64), and so on.
Step 3: Multiply each digit of the octal number by its corresponding position value.
Step 4: Sum up all the products obtained in Step 3.
Step 5: The result is the decimal equivalent of the given octal number.
How to convert Decimal number to octal number system ?
Step 1 Divide the decimal number by 8.
Step 2 Record the remainder
Step 3 Repeat the division with the quotient obtained in the previous step until the quotient is less then 8.
Step 4 The Octal representation is the sequence of remainders read in reverse order.
.
How to convert Hexadecimal number to decimal number ?
Step 1: Write down the hexadecimal number.
Step 2: Assign a position value to each digit of the hexadecimal number, starting from the right and increasing by a power of 16 for each position to the left. The rightmost digit is in the 16^0 position (which equals 1), the next digit to the left is in the 16^1 position (which equals 16), then 16^2 (which equals 256), and so on.
Step 3: Convert any letters in the hexadecimal number to their corresponding decimal values (A is 10, B is 11, C is 12, D is 13, E is 14, and F is 15).
Step 4: Multiply each digit of the hexadecimal number (including the converted letters) by its corresponding position value.
Step 5: Sum up all the products obtained in Step 4.
Step 6: The result is the decimal equivalent of the given hexadecimal number.
.
How to convert Decimal number to Hexadecimal number ?
Step 1 Divide the decimal number by 16.
Step 2 Record the remainder
Step 3 Repeat the division with the quotient obtained in the previous step until the quotient is less then 16.
Step 4 The Hexadecimal representation is the sequence of remainders read in reverse order.
Conclusion









Post a Comment