संख्या प्रणाली और रूपांतरण को समझना

Number Systems Conversions

परिचय संख्या प्रणाली रूपांतरण

आइए संख्या प्रणालियों की आकर्षक दुनिया का पता लगाएं और संख्याओं को दर्शाने के विभिन्न तरीकों की खोज करें। हम सुप्रसिद्ध दशमलव प्रणाली से शुरुआत करेंगे, जहाँ हम दहाई में गिनती करते हैं। इसके बाद, हम बाइनरी में गोता लगाएँगे, जिसमें केवल शून्य और एक का उपयोग होता है, और हेक्साडेसिमल, जिसमें सोलह विभिन्न प्रतीक शामिल होते हैं। ऑक्टल को नज़रअंदाज़ न करें, जिसमें आठ प्रतीक होते हैं! आप सीखेंगे कि संख्यात्मक प्रतिनिधित्व की जटिलताओं को उजागर करते हुए, इन प्रणालियों के बीच कैसे रूपांतरण किया जाए। चाहे आप गणित के प्रति उत्साही हों या बस जिज्ञासु हों, यह यात्रा संख्याओं और उनकी विभिन्न प्रणालियों के बारे में आपकी समझ को बढ़ाएगी। संख्याओं की भाषा जानने के लिए तैयार हो जाइए!

संख्या प्रणालियों को कई तरीकों से एक दूसरे में परिवर्तित किया जा सकता है:

- बाइनरी से दशमलव और इसके विपरीत

- बाइनरी से ऑक्टल और इसके विपरीत

- बाइनरी से हेक्साडेसिमल और इसके विपरीत

- दशमलव से अष्टक और इसके विपरीत

- दशमलव से हेक्साडेसिमल और इसके विपरीत

- ऑक्टल से हेक्साडेसिमल और इसके विपरीत

Number System Conversion

बाइनरी से दशमलव रूपांतरण

किसी बाइनरी संख्या को दशमलव संख्या में बदलने के लिए, इन चरणों का पालन करें:

चरण 1: बाइनरी संख्या लिखें।

चरण 2: बाइनरी संख्या में प्रत्येक अंक का स्थानीय मान पहचानें। सबसे दाहिना अंक "एक" स्थान का प्रतिनिधित्व करता है, बाईं ओर का अगला अंक "दो" स्थान का प्रतिनिधित्व करता है, फिर "चार" स्थान, "आठ" स्थान का प्रतिनिधित्व करता है, और इसी तरह, जैसे-जैसे आप दाएं से बाएं जाते हैं, 2 की शक्ति बढ़ती जाती है।

चरण 3: प्रत्येक अंक को उसके संगत स्थानीय मान से गुणा करें।

चरण 4: दशमलव समतुल्य प्राप्त करने के लिए चरण 3 से सभी परिणामों को जोड़ें।

यहाँ एक उदाहरण है:

आइए बाइनरी संख्या 1101 को दशमलव में बदलें।

चरण 1: बाइनरी संख्या 1101 है।

चरण 2: दाएँ से बाएँ स्थान मान 1 (एक के लिए), 2 (दो के लिए), 4 (चार के लिए), और 8 (आठ के लिए) हैं।

चरण 3: प्रत्येक अंक को उसके स्थानीय मान से गुणा करें:

1 * 1 = 1 (इकाई के स्थान के लिए)

0 * 2 = 0 (दो स्थानों के लिए)

1 * 4 = 4 (चौथे स्थान के लिए)

1 * 8 = 8 (आठवें स्थान के लिए)

चरण 4: परिणाम जोड़ें:

1 + 0 + 4 + 8 = 13

तो, बाइनरी संख्या 1101 दशमलव संख्या 13 के बराबर है।

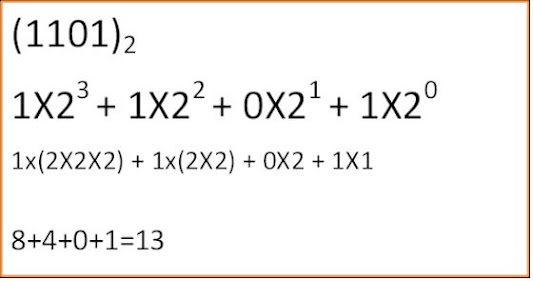Binary To Decimal Conversion

इस प्रकार आप बाइनरी संख्याओं को दशमलव संख्याओं में बदल सकते हैं। स्थानीय मानों को पहचानना सुनिश्चित करें और बाइनरी संख्या में प्रत्येक अंक का दशमलव समकक्ष ज्ञात करने के लिए आवश्यक गुणन करें।

दशमलव से बाइनरी रूपांतरण

दशमलव संख्या को बाइनरी में बदलने में दशमलव संख्या को 2 से विभाजित करने और शेषफल को नोट करने की प्रक्रिया शामिल होती है। इसे चरण दर चरण कैसे करें यहां बताया गया है:

चरण 1: दशमलव संख्या को 2 से विभाजित करें।

चरण 2: शेषफल लिखिए (जो या तो 0 या 1 होगा)।

चरण 3: पिछले चरण के भागफल को 2 से विभाजित करना जारी रखें जब तक कि भागफल 0 तक न पहुँच जाए।

चरण 4: अवशेषों को उल्टे क्रम में पढ़कर द्विआधारी निरूपण बनता है।

उदाहरण के लिए, आइए दशमलव संख्या 125 को बाइनरी में बदलें।

125 को बाइनरी में बदलने के लिए, इन चरणों का पालन करें:

1. संख्या को 2 से विभाजित करें.

2. शेषफल नोट करें.

3. इसे नए भागफल के साथ तब तक दोहराएँ जब तक यह 0 न हो जाए।

4. द्विआधारी निरूपण उल्टे क्रम में पढ़ा गया शेषफल है।

अब, आइए इन चरणों को 125 पर लागू करें:

125 ÷ 2 = 62 शेष 1 के साथ (यह सबसे कम महत्वपूर्ण बिट है)

62 ÷ 2 = 31 शेषफल 0 के साथ

31 ÷ 2 = 15 शेष 1 के साथ

15 ÷ 2 = 7 शेष 1 के साथ

7 ÷ 2 = 3 शेष 1 के साथ

3 ÷ 2 = 1 शेषफल 1 के साथ

1 ÷ 2 = 0 शेष 1 के साथ (यह सबसे महत्वपूर्ण बिट है)

अब यदि हम शेषफल को उल्टे क्रम में पढ़ें तो हमें 1111101 प्राप्त होता है।

Decimal To Binary Conversion

इसलिए, 125 का द्विआधारी प्रतिनिधित्व 1111101 है।

अष्टक से दशमलव संख्याओं का रूपांतरण

अष्टक और दशमलव दो अलग-अलग अंक प्रणालियाँ हैं।

ऑक्टल 8 के आधार पर संचालित होता है, जिसका अर्थ है कि इसमें केवल 0 से 7 तक के अंक शामिल हैं।

इसके विपरीत, दशमलव 10 के आधार का उपयोग करता है, जिसमें 0 से 9 तक के अंक होते हैं।

किसी अष्टक संख्या को दशमलव संख्या में बदलने के लिए, आप इन चरणों का पालन कर सकते हैं:

चरण 1: अष्टक संख्या लिखिए।

चरण 2: अष्टक संख्या के प्रत्येक अंक के लिए एक स्थिति मान निर्दिष्ट करें, दाईं ओर से शुरू करें और बाईं ओर प्रत्येक स्थिति के लिए 8 की शक्ति से बढ़ाएं। सबसे दाहिना अंक 8^0 स्थिति में है (जो 1 के बराबर है), बाईं ओर का अगला अंक 8^1 स्थिति में है (जो 8 के बराबर है), फिर 8^2 (जो 64 के बराबर है), और इसी तरह आगे भी।

चरण 3: अष्टक संख्या के प्रत्येक अंक को उसके संबंधित स्थिति मान से गुणा करें।

चरण 4: चरण 3 में प्राप्त सभी उत्पादों को एक साथ जोड़ें।

चरण 5: परिणाम दिए गए अष्टक संख्या के दशमलव समकक्ष होगा।

आइए प्रक्रिया को स्पष्ट करने के लिए एक उदाहरण का उपयोग करें। हम अष्टक संख्या 346 को उसके दशमलव समकक्ष में परिवर्तित करेंगे:

चरण 1: अष्टक संख्या 346 है।

चरण 2: स्थिति मान निर्दिष्ट करें: 6 8^0 स्थिति में है, 4 8^1 स्थिति में है, और 3 8^2 स्थिति में है।

चरण 3: प्रत्येक अंक को उसके स्थान मान से गुणा करें:

6 * 8^0 = 6 * 1 = 6

4 * 8^1 = 4 * 8 = 32

3 * 8^2 = 3 * 64 = 192

चरण 4: परिणाम जोड़ें: 6 + 32 + 192 = 230

चरण 5: इसलिए, अष्टक संख्या 346 का दशमलव समतुल्य 230 है।

इस प्रकार, अष्टक संख्या 346 दशमलव संख्या 230 से मेल खाती है।

Octal to Decimal numbers Conversion

दशमलव से अष्टक रूपांतरण:

दशमलव संख्या को अष्टक में बदलने के लिए, हम भाग और शेषफल की विधि का उपयोग कर सकते हैं।

2 से विभाजित करने के बजाय, हम 8 से विभाजित करते हैं और शेषफल का हिसाब रखते हैं।

हम इस प्रक्रिया को भागफल के साथ तब तक जारी रखते हैं जब तक कि कोई और भागफल न रह जाए।

फिर दशमलव संख्या के अष्टक समतुल्य ज्ञात करने के लिए शेषफलों को उल्टे क्रम में व्यवस्थित किया जाता है।

चरण 1: दशमलव संख्या को 8 से विभाजित करें।

चरण 2: शेष को रिकॉर्ड करें।

चरण 3: पिछले चरण के भागफल के साथ विभाजन को तब तक दोहराएँ जब तक कि भागफल 8 से कम न हो जाए।

चरण 4: अष्टक निरूपण उल्टे क्रम में पढ़े गए शेषफलों का क्रम है।

उदाहरण के लिए,

दशमलव संख्या 30 को अष्टक में बदलने के लिए, हम 30 को 8 से विभाजित करते हैं, जिसके परिणामस्वरूप भागफल 3 और शेषफल 6 होता है।

इसके बाद, हम 3 का भागफल लेते हैं और इसे फिर से 8 से विभाजित करते हैं, जिससे हमें 0 का भागफल और 3 का शेषफल मिलता है।

शेषफलों को उल्टे क्रम में व्यवस्थित करने से हमें 30 का अष्टक समतुल्य प्राप्त होता है, जो कि 36 है।

Decimal to Octal Conversion:

हेक्साडेसिमल से दशमलव संख्या में रूपांतरण

हेक्साडेसिमल और दशमलव दो अलग-अलग अंक प्रणालियाँ हैं।

हेक्साडेसिमल 16 के आधार पर संचालित होता है, जिसका अर्थ है कि इसमें 0 से 9 तक अंक और ए से एफ तक अक्षर शामिल हैं। इस प्रणाली में, ए का मतलब 10, बी का मतलब 11 और इसी तरह आगे एफ तक है, जो 15 का प्रतिनिधित्व करता है।

दूसरी ओर, दशमलव 10 के आधार का उपयोग करता है, जिसमें 0 से 9 तक के अंक होते हैं।

हेक्साडेसिमल संख्या को दशमलव संख्या में बदलने के लिए, आप इन चरणों का पालन कर सकते हैं:

चरण 1: हेक्साडेसिमल संख्या लिखें.

चरण 2: हेक्साडेसिमल संख्या के प्रत्येक अंक के लिए एक स्थानीय मान निर्दिष्ट करें, दाईं ओर से शुरू करें और बाईं ओर प्रत्येक स्थिति के लिए 16 की शक्ति से बढ़ाएं। सबसे दाहिना अंक 16^0 स्थिति में है (जो 1 के बराबर है), बाईं ओर का अगला अंक 16^1 स्थिति में है (जो 16 के बराबर है), फिर 16^2 (जो 256 के बराबर है), और इसी तरह।

चरण 3: हेक्साडेसिमल संख्या में किसी भी अक्षर को उनके संगत दशमलव मान में बदलें (ए 10 है, बी 11 है, सी 12 है, डी 13 है, ई 14 है, और एफ 15 है)।

चरण 4: हेक्साडेसिमल संख्या के प्रत्येक अंक (परिवर्तित अक्षरों सहित) को उसके संबंधित स्थानीय मान से गुणा करें।

चरण 5: चरण 4 में प्राप्त सभी उत्पादों का योग करें।

चरण 6: परिणाम दिए गए हेक्साडेसिमल संख्या के दशमलव समकक्ष होगा।

उदाहरण के लिए, आइए हेक्साडेसिमल संख्या 1A3 को उसके दशमलव समकक्ष में बदलें: 

चरण 1: हेक्साडेसिमल संख्या 1A3 है। 

चरण 2: स्थिति मान निर्दिष्ट करें: 3 16^0 स्थिति में है, ए 16^1 स्थिति में है, और 1 16^2 स्थिति में है। 

चरण 3: अक्षर A को उसके दशमलव मान में बदलें, जो 10 है। 

चरण 4: प्रत्येक अंक को उसके स्थिति मान से गुणा करें: 3 * 16^0 = 3 * 1 = 3 ए * 16^1 = 10 * 16 = 160 1 * 16^2 = 1 * 256 = 256 चरण

 5: परिणाम जोड़ें: 3 + 160 + 256 = 419

 चरण 6: इसलिए, हेक्साडेसिमल संख्या 1ए3 का दशमलव समतुल्य 419 है। निष्कर्ष में, हेक्साडेसिमल

Hexadecimals to Decimal numbers Conversion

दशमलव से हेक्साडेसिमल रूपांतरण

हेक्साडेसिमल और दशमलव दो अलग-अलग अंक प्रणालियाँ हैं।

हेक्साडेसिमल 16 के आधार पर संचालित होता है, जिसका अर्थ है कि इसमें 0 से 9 तक अंक और ए से एफ तक अक्षर शामिल हैं। इस प्रणाली में, ए का मतलब 10, बी का मतलब 11 और इसी तरह आगे एफ तक है, जो 15 का प्रतिनिधित्व करता है।

दूसरी ओर, दशमलव 10 के आधार का उपयोग करता है, जिसमें 0 से 9 तक के अंक होते हैं।

हेक्साडेसिमल संख्या को दशमलव संख्या में बदलने के लिए, इन चरणों का पालन करें:

चरण 1: हेक्साडेसिमल संख्या लिखें.

चरण 2: हेक्साडेसिमल संख्या के प्रत्येक अंक के लिए एक स्थानीय मान निर्दिष्ट करें, दाईं ओर से शुरू करें और बाईं ओर प्रत्येक स्थिति के लिए 16 की शक्ति से बढ़ाएं। सबसे दाहिना अंक 16^0 स्थिति में है (1 के बराबर), बाईं ओर का अगला अंक 16^1 स्थिति में है (16 के बराबर), फिर 16^2 (256 के बराबर), और इसी तरह।

चरण 3: हेक्साडेसिमल संख्या में किसी भी अक्षर को उनके संगत दशमलव मान में बदलें (ए 10 है, बी 11 है, सी 12 है, डी 13 है, ई 14 है, और एफ 15 है)।

चरण 4: हेक्साडेसिमल संख्या के प्रत्येक अंक (परिवर्तित अक्षरों सहित) को उसके संबंधित स्थानीय मान से गुणा करें।

चरण 5: चरण 4 में प्राप्त सभी उत्पादों का योग करें।

चरण 6: परिणाम हेक्साडेसिमल संख्या के दशमलव समकक्ष होगा।

Decimal to Hexadecimal Conversion

अक्सर पूछे जाने वाले प्रश्न(FAQ)

• बाइनरी संख्या को दशमलव संख्या में कैसे बदलें?
• दशमलव संख्या को बाइनरी संख्या में कैसे बदलें?
• ऑक्टल संख्या को दशमलव संख्या में कैसे बदलें?
• दशमलव संख्या को अष्टक संख्या प्रणाली में कैसे बदलें?
• हेक्साडेसिमल संख्या को दशमलव संख्या में कैसे बदलें?
• दशमलव संख्या को हेक्साडेसिमल संख्या में कैसे बदलें?

निष्कर्ष

अंत में, यह ब्लॉग संख्या और उनकी रूपांतरण विधि को कवर करता है, संक्षेप में, मैं कह सकता हूं कि संख्या प्रणाली कितनी महत्वपूर्ण हैं, वे प्रौद्योगिकी और गणित दोनों में महत्वपूर्ण भूमिका निभाते हैं। इस ब्लॉग में निम्नलिखित विषयों का संक्षिप्त विवरण शामिल है

• बाइनरी से दशमलव और इसके विपरीत
• बाइनरी से ऑक्टल और इसके विपरीत
• बाइनरी से हेक्साडेसिमल और इसके विपरीत
• दशमलव से अष्टक और इसके विपरीत
• दशमलव से हेक्साडेसिमल और इसके विपरीत
• ऑक्टल से हेक्साडेसिमल और इसके विपरीत

संक्षेप में, मैं कह सकता हूं कि ये विषय उन लोगों के लिए बहुत उपयोगी हैं जो विभिन्न विश्वविद्यालयों से बीसीए, पीजीडीसीए, डीसीए, 'ओ' लेवल पाठ्यक्रम कर रहे हैं।